Contents:
Concept of growth
- Growth is defined as the synthesis of a new protoplasmic constituent by a cell. A cell may then undergo division to give rise to new cells.
- In unicellular organisms, growth follows division in which there is an increase in the number of cells. In a multicellular organism, growth is followed by an increase in cell size and weight. In unicellular organisms such as bacteria, the growth period is relatively short due to its small size. In order to maintain this small size, bacteria must reproduce.
- Growth is an irreversible process that occurs at all organizational levels.
- There are three patterns of growth.
1. Auxetic growth – an increase in cell mass.
2. multiplicative growth – an increase in cell number due to cell division.
3. Accretionary growth – growth due to the accumulation of extracellular products.
Reproduction
1) Binary fission – Binary fission is the form of asexual reproduction in single-celled organisms, used by most prokaryotes. This process results in the reproduction of a living cell by division into two equal or near-equal parts.
Organisms that reproduce through binary fission generally have exponential growth phases. Escherichia coli cells are able to divide every 20 minutes under optimum conditions during their exponential growth phase.
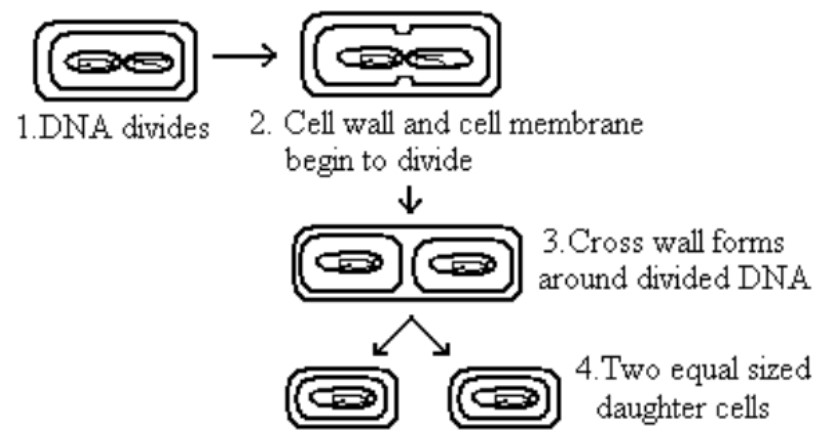
Process: The steps in binary fission are as follows:
a) Initiation period (I period): It is a preparative period for fission. The cells are slightly elongated.
b) C Period – The end of the Initial period, signals the initiation of the C period. During this period the bacterial chromosome replicates. Proteins that are needed for the division are also synthesized.
c) D Period – The D (division) period beings when the nuclear material is evenly distributed. The plasma membrane near the cell pinches inward. The cell wall thickness grows inward at the same point, forming a transverse wall. Finally, a parent cell divides to produce two equal-sized progeny cells. The fissions process in Gram-negative and Gram-positive cells differs slightly. For example, binary fission is found in bacteria such as Bacillus subtilis, Streptococcusfaecalis, etc.
2) Budding – Some bacteria divide by budding e.g. Rhodopseudomonas acidophila. In budding, a small protuberance (bud) develops at one end of the cell. It enlarges and eventually develops into a new cell, which separates from the parent cell.

3) Fragmentation- Bacteria that produce filamentous growth, such as Nocardia species, reproduce by fragmentation. During reproduction, there is the fragmentation of fi laments to produce bacillary or coccoid forms each of which grows as individual cells.

4) Multiple fission – Division of the nucleus, simultaneously or successively, into a number of daughter nuclei, followed by division of the cell body into an equal number of parts, each containing a nucleus.
Mathematical expression of Bacterial growth
- A bacterial culture undergoing balanced growth mimics a first-order chemical reaction i.e. the rate of increase in bacteria at any particular time is proportional to the number or mass of bacteria present at that time.
- The growth rate (R) of a cell is how rapidly a cell increases in mass. It can be used to determine how long the cell is likely to live before producing another generation. The generation time (g) is defined as the time required for a cell to divide and its population to get double. Different microorganisms have different generation time.
|
Organism |
Generation time(hr) |
| Escherichia coli | 0.20 |
| Treponema pallidum | 330 |
| Bacillus subtilis
Mycobacterium tuberculosis |
0.43
6 |
| Vibrio marinus | 1.35 |
| Yeast | 1.7 |
- Similarly, generation time is not the same for a particular organism under all conditions. It is strongly dependent upon nutrients and environmental conditions. The faster a cell metabolizes nutrients, the shorter its generation time.
Under optimum conditions, microorganisms increase in number by binary fission. The binary fission results in the formation of two daughter cells from each parent cell. Thus, if we start with a single bacterium, the increase in population is by geometric progression.
1——>2——>4 ——>8 ——> 16——> 32 ——>64 ——> 128 ——>256——>
Or
2 ——> 21 ——>22 ——>23 ——>24——>25——>26 . .. . .. 2n
(where n = number of generations)
The increase in number by a constant doubling of cells in a population 1s known as exponential or logarithmic growth.
Calculation for generation time and growth rate
To calculate the generation time of individual microorganisms we should know
1) The number of organisms present at the beginning
2) The number of organisms present at the end of a given time interval and
3) The time interval
If during each succeeding generation, it is assumed as no cell death occurs and the population doubles, the total population (Bn) at the end of the given time is expressed as-
Bn = 1 x 2n (where 2n is the bacterial population after ” n” generations).
However, under practical conditions, several thousands of bacteria (Bo) are introduced into the medium at zero time and not 1, so the equation now becomes-
Bn = Bo x2n .. . . . . . . .. .. . .. . . . .. . .. .. .. . .. .. (1)
Solving equation 1 for n we have:
Log = log Bo + n log 2 …. .. .. . .. .. …… . …. .. …… (2)
But log 2 = 0.301 Hence equation 2 becomes
orn = 3.3 (log Bn – log Bo) …. … …… . ……… . … …… (3)
This equation can give the number of generations (n) occurring at a particular time (t).
Generation time (g) can be determined as: g = t/n
Since, n = 3.3 (log Bn – log Bo )
During exponential growth, the growth rate (R) is:
R = 1/g